

We know that the limit of both -1/x and 1/x as x approaches either positive or negative infinity is zero, therefore the limit of sin(x)/x as x approaches either positive or negative infinity is zero.(f(x)+g(x))=L+M\).Ĭhoose \(δ_1>0\) so that if \(00\) so that if \(00\),ģ. Since sin(x) is always somewhere in the range of -1 and 1, we can set g(x) equal to -1/x and h(x) equal to 1/x. So, to make calculations, engineers will approximate a function using small differences in the function and then try and calculate the derivative of the function by having smaller and smaller spacing in the function sample intervals. In mathematics, a limit is the value that a function (or sequence) approaches as the input (or index) approaches some value. Limits are also used as real-life approximations to calculating derivatives. How Are Calculus Limits Used in Real Life? The one-sided *right* limit of f at x=0 is 1, and the one-sided *left* limit at x=0 is -1. For example, f(x)=|x|/x returns -1 for negative numbers, 1 for positive numbers, and isn't defined for 0. This is a formulation of the intuitive notion that we can get as close as we want to L. How Do You Know if a Limit Is One-Sided?Ī one-sided limit is a value the function approaches as the x-values approach the limit from *one side only*. The epsilon-delta definition of limits says that the limit of f (x) at xc is L if for any >0 theres a >0 such that if the distance of x from c is less than, then the distance of f (x) from L is less than. Limit, a mathematical concept based on the idea of closeness, is used primarily to assign values to certain functions at points where no values are defined, in such a way as to be consistent with nearby values. When Can a Limit Not Exist?Ī common situation where the limit of a function does not exist is when the one-sided limits exist and are not equal: the function "jumps" at the point. The idea of a limit is the basis of all differentials and integrals in calculus. What Are Limits in Calculus?Ī limit tells us the value that a function approaches as that function's inputs get closer and closer(approaches) to some number. If these values tend to some definite unique number as x tends to a, then that obtained a unique number is called the limit of f(x) at x = a.

If at a point x = a, f(x) takes indeterminate form, then we can consider the values of the function which is very near to a. Learn how we define the derivative using limits. Another common interpretation is that the derivative gives us the slope of the line tangent to the functions graph at that point. Limits formula:- Let y = f(x) as a function of x. The derivative of a function describes the functions instantaneous rate of change at a certain point.
#Definition of limit calculus examples how to#
Second example: you know how to define the area of a rectangle (a garden plot, a sidewalk).as the product of the length and width. Here are some properties of the limits of the function: If limits \( \lim _\)įAQs on Limits What is the Limit Formula? Well, calculus defines it as the limit of the change in distance traveled in a time period as the time period becomes smaller. Let us discuss the definition and representation of limits of the function, with properties and examples in detail. Whereas indefinite integrals are expressed without limits, and it will have an arbitrary constant while integrating the function.
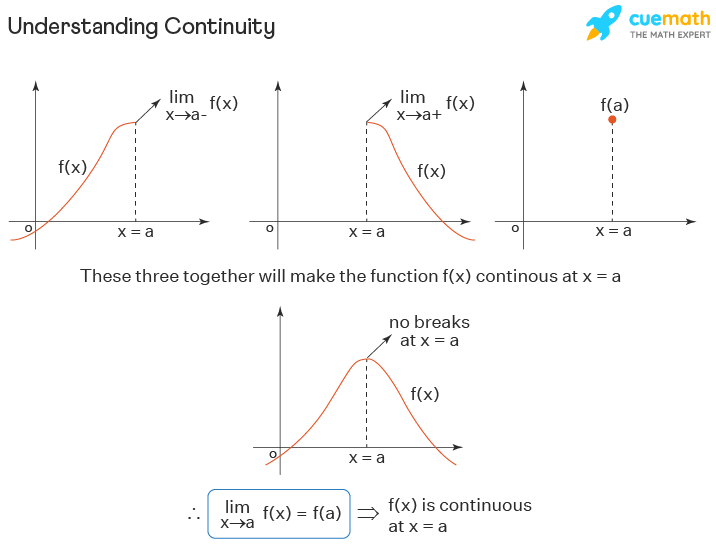
For definite integrals, the upper limit and lower limits are defined properly. Generally, the integrals are classified into two types namely, definite and indefinite integrals. The limit of a sequence is further generalized in the concept of the limit of a topological net and related to the limit and direct limit in the theory category. Infinite Limits and Rational Functions A Rational Function is one that is the ratio of two polynomials: f(x) P(x)Q(x) For example, here P(x) x3 + 2x. It is used in the analysis process, and it always concerns the behavior of the function at a particular point. Limits play a vital role in calculus and mathematical analysis and are used to define integrals, derivatives, and continuity. Limits in maths are defined as the values that a function approaches the output for the given input values.


 0 kommentar(er)
0 kommentar(er)
